Google 是如何设计排名系统的

本文讲述谷歌云工程师如何协助它的客户解决排名系统难题的文章，这篇文章里面涉及了算法和工程的优秀结合，非常值得一读。

准确排名

谷歌的一名大客户 Applibot 在开发游戏 Legend of the Criptids 的过程中遇到一个排名的难题：

游戏中有数十万甚至更多的玩家同时在线。当一个玩家击倒敌人（或者其他行为）的时候，它们的分数会改变，如何在游戏中显示最新的玩家排名？

计算排名很简单，不过扩展性和效率并不高，例如，你可以在数据库直接查询：

SELECT count(key) FROM Players WHERE Score > YourScore 

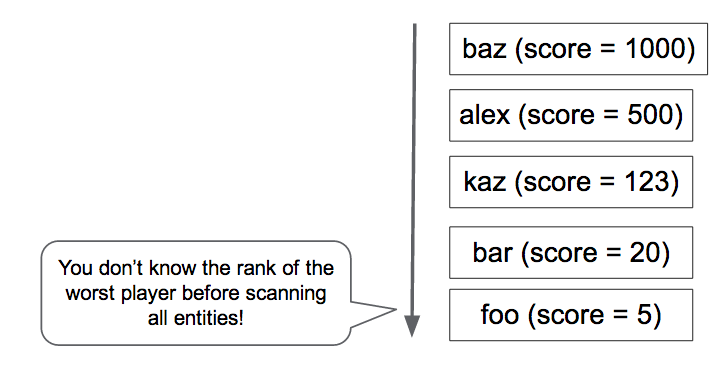
这个查询会返回大于你的分数的玩家数量，一开始，Applibot 的工程师 Tomoaki 就是选用了这个方案，他发现查询花费了几秒钟才得到响应，这个方案实在太慢与太耗费资源，而且当玩家越多的时候，问题也会更加严重。当你的游戏有一百万在线玩家的话，你一定不会想每个玩家在查找排名的时候都像这样查询一次数据库。接着，Tomoaki 想到第二个方案，用 Memcache 维护这些排名数据，这样会更加快速高效，但是并不可靠，Memcache 存储的对象随时会被删除，事实上，Memcache 本身也不太可靠。一个排名系统仅仅依靠 Memcache，非常难去保证它的一致性与可靠性。最后，Tomoaki 还想到一个临时方案，他决定退而求其次，与其每次请求都计算排名，他使用了一个定时器每个小时定时计算并且更新用户排名。这样的话每次请求都能很快得到结果，但是这个排名会有一个小时的延迟。

像大部分程序员一样，Tomoaki 想找一个快速可靠的，可以接受每秒 300次 更新并且能在数百毫秒内返回结果的排名系统方案。这个时候，Tomoaki 找到 Kaz Sato，谷歌的方案架构师，希望他可以帮助解决这个问题。Kaz Sato 知道排名是一个在大型分布式系统中经典而且难解的问题，他开始在谷歌云中去找寻解决方案。

log(n) 的解决方案

一开始的方案，数据库查询需要扫描一遍所有的玩家的得分才能计算出排名，（注释：虽然数据库能提供缓存，但是由于游戏系统中，玩家的得分更新很快。所以使用缓存会得到不准确的排名。）它的算法时间复杂度为 O(n)，也就是说随着玩家越来越多，运行时间也会同比增长。所以，我们需要一个 O(log(n)) 或者更快的算法，让运行时间仅仅以对数级别增长。如果你曾经学过计算机科学，这时候可能就会想到树数据结构，例如二叉树，红黑树或者 B 树，能够在 O(log(n)) 的时间内找到一个元素。并且通过在节点中存储数据可以进行计数，极值查找，平均值查找。使用树结构可以在 O(log(n)) 时间内实现这个排名系统，kaz 接下来找到一个谷歌的开源项目，这个开源库实现了两个功能：

• SetScore 设定玩家的分数
• FindRank 获取分数对应的排名

Kaz 使用了 Apache JMeter 作为压测工具对这个开源库进行测试，发现使用这个树算法之后，更新分数和查找排名都能在数百毫秒内完成。

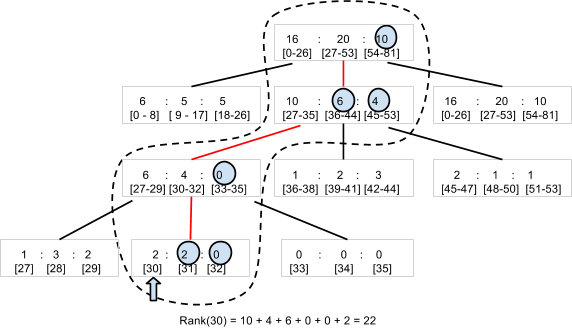
注释：这个开源项目实现了一个 N-ary 树，类似 Segment 树的变形。每个节点存储三个对应的区间内的分数，不过这里我们并不讨论这个方案，因为这种数据结构实在太特殊，一般编程语言都没有实现。我们在本文中使用另外一个常见的数据结构，二叉平衡树来解决这个问题。为什么不使用堆呢？堆也有排序以及找第 k 大元素的作用，不过堆要找第 k 个元素的话需要 pop k 次，之后还要把 pop 的元素添加回来。对于需要频繁更新的元素来说并不合适。

以下为实现细节，如果你不感兴趣的话可以跳过。二叉平衡树的每个节点额外记录左右子树的节点数量，同样能在 O(log(n))时间内完成。

1. 初始化，建立一个哈希表，键为玩家 ID，值为分数对象，ID-> 分数对象，时间为 O(n)。接下来，建立一个以（分数对象，ID）为大小的全部玩家数量 n 的二叉平衡树，其中每个节点额外记录左右子树的节点数量。建立数据结构的时间为 O(nlog(n))。
2. 要找到某个玩家的排名，我们只需要在哈希表中查找对应 ID 的分数对象的值 ，然后在二叉平衡树中根据其左节点以及父节点的左节点数量递归找到对应排名，时间为 O(log(n))。
3. 要找到某个区间内的排名，例如第 101 到 第 200 名，我们需要查找 100 次对应排名的玩家，时间为 O(k(log(n))，其中 k 为区间的大小。
4. 更新玩家分数：更新哈希表，并且更新二叉平衡树的节点，时间为 O(log(n))。

并发更新的问题

但是在压力测试的过程中， Kaz 发现了开源库的一个问题，它对于并发更新的可扩展性非常弱，当他尝试着把请求压力提高到每秒 3次 更新的时候，更新就开始返回错误异常了。很明显，这与 Applibot 要求的能支持每秒 300次 更新还有很大的距离。那么原因是什么呢？一般来说，树结构并不是线性安全的，所以此开源库需要维护树结构的强一致性，也就是保证每次只更新一个节点。而由于整个解决方案基于谷歌的 Datastore，一个高性能的非关系型数据库，（注释：树结构都存储在这个数据库中）。Datastore 使用事务来保证强一致性，每个对象最多只能支持每秒 1次事务执行，当有高并发更新请求的时候，每次更新都需要执行一次事务，最后导致吞吐量非常低。

任务合并

Kaz 想起之前 Datastore 团队提出过的一个方案，与其每次更新都执行 1次 事务，可以尝试把多个更新操作合并一起再执行 1次 事务。不过这样每个事务可能包含大量的更新，花费的时间也更久，而在 1次 事务中执行多个更新的话，会增加了并发冲突的可能性。有鉴于此，Datastore 团队提出了另外一个方案，基于队列的任务合并，这个设计模式在 VoltDb 和 Redis 都能看到，简单来说，就是使用单线程在一次事务中按顺序执行这些更新，既然是单线程，那么就不会有并发冲突的问题。不过，也因为每次只有一个线程在执行任务，更新的速度就取决于这个线程执行更新的速度，需要使用工具测试能否支持每秒 300 次更新。基于这个方案，Kaz 实现了任务合并方案的代码，包括以下几部分：

• 前端：接受 SetScore 请求，并把任务放到队列
• 队列：持续接受保存前端发过来的 SetScore 请求
• 后端：使用单线程无限循环，不断把队列里的请求拿出来进行合并，然后使用开源库执行，每次执行都是 1次 事务。

Kaz 再次使用 JMeter 进行测试，他证明了这个方案能够支持每秒 200次 更新，每次事务执行 500 到 600 次更新。（注释：每个事务可能会执行超过一秒钟）

任务合并的稳定性

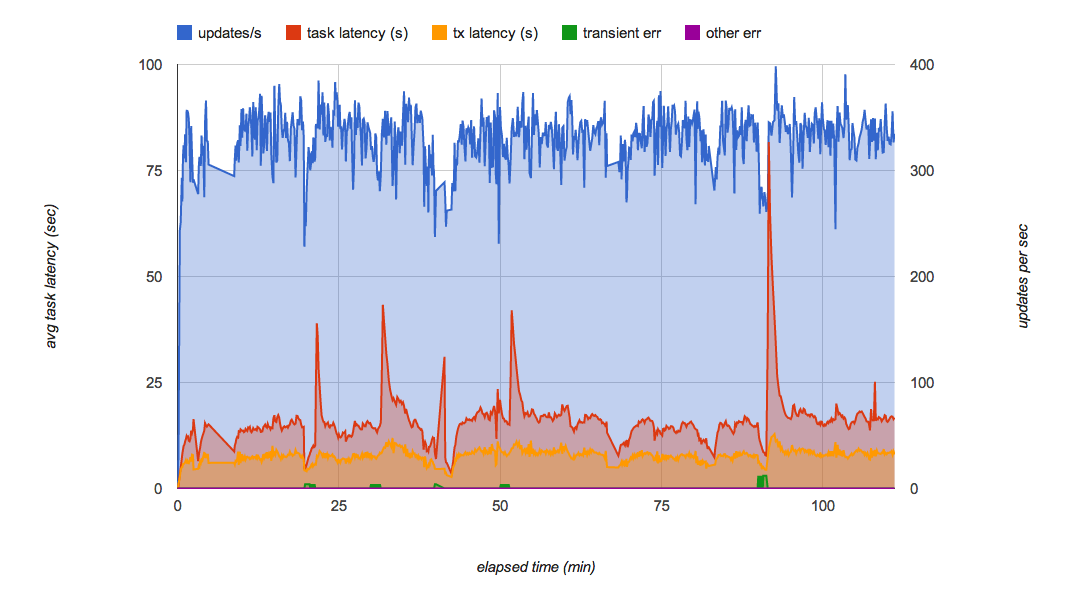
但是 Kaz 发现了另外一个问题，但他使用这个方案运行测试几分钟的时候，发现队列的吞吐量偶尔会大范围波动（如下图），尤其是持续几分钟，每秒放入队列 200 个任务的时候。队列突然停止分发任务给后端了，致使响应时间大幅提高。

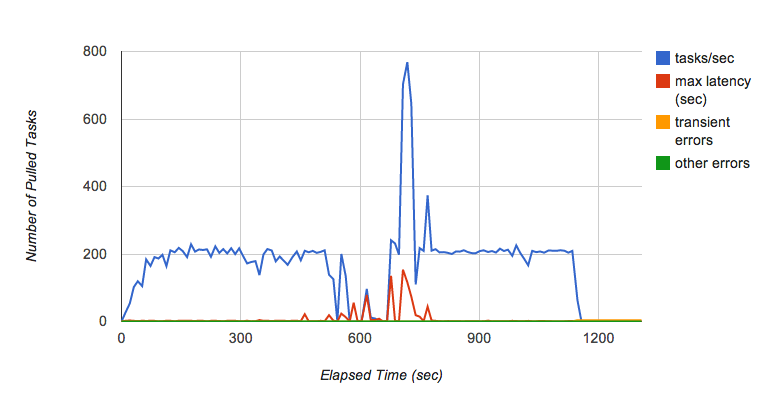
Kaz 咨询其他团队问题的来源，发现这已经是个老问题了，因为队列服务使用了 Bigtable 作为持久层，但 Bigtable 的分片过大的时候，会分成多个分片。而在分片的过程，任务是不会进行分发的，所以就导致了上面这个问题。这时候 Michael Tang，一位方案架构师，提出使用多个队列来执行任务，这样即使一个队列因为过大而需要分片时，其他队列也能提供服务，改进后的架构如下：

1. 把 SetScore 任务放到 10个 队列中
2. 使用另外一个方法 SetScores 从队列中获取任务并且合并，分发给后端
3. 从队列中删除执行成功的任务

第一步，每一个队列最多存放 1000个 任务，每个任务里面包含了玩家名和分数，我们从队列中拿到信息后，把这些信息中包含的玩家和分数的组合合并放到一个字典（合并更新）。第二步，使用开源库的更新操作来进行更新树结构，开源库会开启一个事务执行这些操作并把他们存储在 Datastore 里面。如果任务执行成功的话，那么就把任务从队列中删除。如果任务执行失败的话，更新操作还会留在队列中，之后还可以重新执行一次。在实际环境中，你可能需要类似 Watchdog 这样的工具来监控更新情况。下图显示了这个新方案的实现效果，它能最大程度地利用资源并且能持续多个小时支持每秒 300次更新，这个最终方案达到了 Applibot 原本的所有要求：

• 能支持数十万甚至更多的玩家
• 能够保证持久化以及一致性，因为所有更新都是通过 Datastore 的事务进行更新。
• 能支持每秒 300次更新

对这个方案进行总结，有以下优缺点：

优点:

• 高效快速：能在数百毫秒内找到玩家排名以及进行更新
• 强一致性以及持久化
• 排名准确
• 可以扩展到任意数量的玩家

缺点：

• 吞吐量有限制，只能支持约每秒 300次更新。因为这个解决方案依赖于一个单线程执行合并之后的更新。

使用分片树进行扩展

如果你需要支持更高的并发更新量，你可以对树结构进行分片，同时需要对系统进行一些修改，例如指定某些队列专门更新某个树结构的分片。在最简单的情况下，SetScore 更新会随机分配给一个队列，使用分片后的三棵树的话，能够提高三倍的吞吐量（注释：按照我的理解以及对开源库源码的分析， SetScore 是需要先找到对应的玩家所在的树然后进行更新的）。相应的产生的问题是，在调用 FindRank 计算排名的时候，需要查找三棵树最后把排名加起来。例如 FindRank(865) 可能会在三棵树分别排名在 124，183 以及 156。代表三棵树分别有那么多玩家分数比 865 高。所以这个分数的最终排名应该是 124 + 183 + 156 = 463。这种方式并不适合所有的分布式系统，但是因为排名是可累计的，所以能够这样设计。

近似排名

常见算法如下，本文会讨论第一种以及第三种：

• Lossy Counting Method
• Frugal Streaming
• Buckets with Global Query

Lossy Counting Method

算法本身的作用是**找出长度为 N 的数据流中出现频率超过 s % 的元素，保证误差小于 a %。**其中 s 与 a 是传入的参数，a 一般设定为 s 的十分之一。此算法从数学上保证：

1. 在数据流中，出现频率高于 s * N 的元素最后都会输出。
2. 在数据流中，如果出现频率低于 ( s - a ) * N 的元素不会被输出。
3. 估算的出现次数与实际次数的差距不会高于 a * N。

算法实现起来也相对简单，只有三步：

1. 把现有的数据分成 N 个窗口，每个窗口的大小为 1 / a。
2. 按顺序统计每一个窗口里面元素出现的个数并减去 1。
3. 把剩下的值加起来并且返回所有大于 ( s - a ) * N 的值。

让我们用个例子来解释，假设现有的数据是 10 万条，要找出出现频率为 1% 以上，也就是 1000 条以上的元素，并要求误差小于 0.1 %。

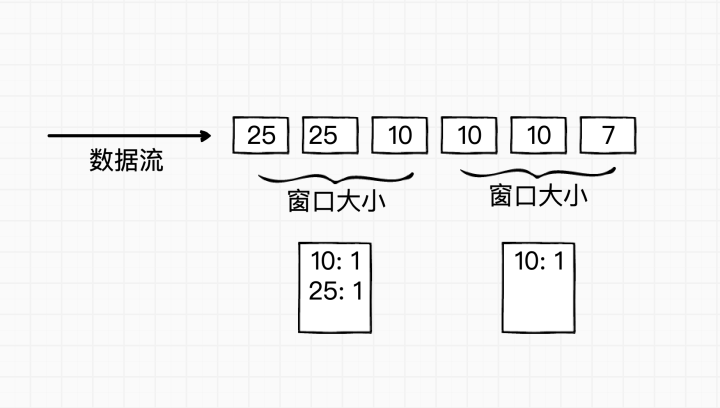
1. 把现有数据分成 1000 个窗口，每个窗口大小为 100。
2. 建立一个（元素，频率）的哈希表 V，默认为空。从窗口 1 开始，统计每个元素出现的频率，如果元素不在哈希表 V，则记录（元素，1），反之则把哈希表 V 中该元素的频率加 1。
3. 每个窗口统计结束后，把哈希表 V 中所有元素的频率都减去 1。若此时某元素的频率变成 0 则从哈希表 V 中删除，重复此步骤按顺序统计剩下的窗口。

这个算法有点类似桶排序，不过因为我们每次进行窗口统计之后都丢弃频率为 1 的元素，所以我们的哈希表中不需要记录所有元素，节省了大量内存。那我们怎么利用这个算法计算 SetScore和 FindRank呢？

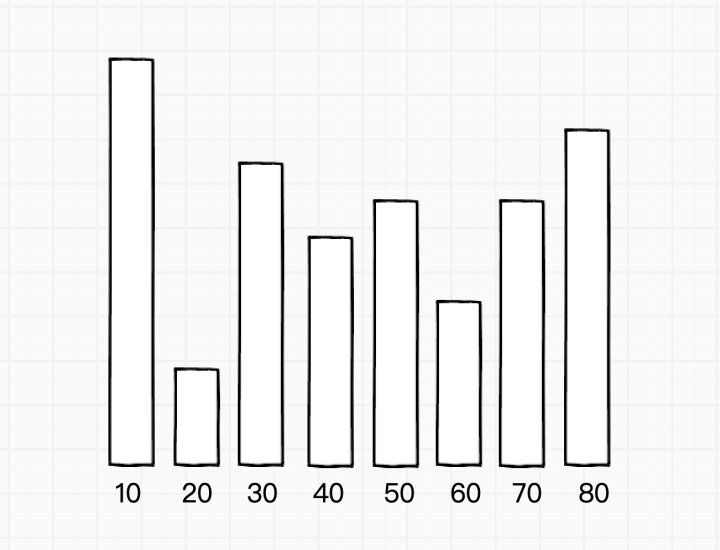
• 算法结束后，我们得到了记录（元素，频率）的哈希表 V，从下图中，我们可以看到元素 10 出现的频率最高：

• 建立一个玩家和分数对应的另一个哈希表 T。
• SetScore ：当需要更新玩家分数的时候，例如把用户 A 更新为 30 分。1) 先从哈希表 T 中找到用户 A 的旧分数，2) 更新哈希表 T 中用户 A 的分数为 30 分，3) 从 V 中把旧分数对应的频率减 1（如果没出现就不用减），如果分数为 0 则从 V 中删除，4) 然后把 30 分 对应的频率加 1。
• FindRank ：如果需要找 30 分的排名，只需要在哈希表内把 大于 30 的元素频率都加起来即可。

优点：

• 容易实现以及修改，能够控制元素频率以及误差。
• 快速高效，建立哈希表 V 只需要遍历一遍数据即可。
• 这个算法也适用于“如何设计一个显示最热门的 100个 标签的系统“这类场景。

缺点：

• 这个算法适用于玩家分布比较集中的情况，也就是说有很多玩家的分数是相同的。如果玩家的分数都不同，或者分布零散的话，哈希表 V 需要内存维护大量元素，会退化成桶排序。
• FindRank需要在哈希表 V 中遍历所有比该分数大的桶。

Buckets with Global Query

另外一个方法是把分数按照不同区间放在桶内，在测试中，我们能在 400 毫秒内得到任意用户的排名，其中包括了 HTTP 请求和返回的时间，其中 FindRank的时间并不会由于玩家数量改变而改变。 假设玩家分数分布在 [0, 99]，我们设定 4个 区间，每个区间需要记录频率以及当前区间最高分数所在的排名：

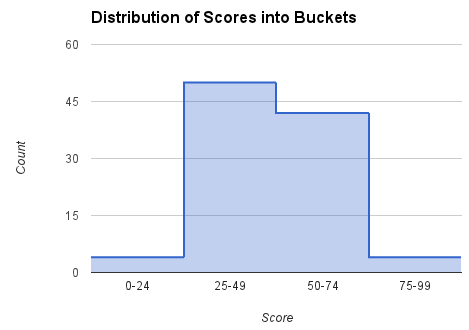
我们会使用这些信息来计算分数的排名，例如如果玩家的分数是 60，我们会查找对应的 [50, 74] 区间，使用该区间的频率 42 和该区间最高排名（74分的排名是5）来估计排名，公式如下：

rank = 5  + (74 - 60)*42/(74 - 50) =  30

（注释：因为当区间内分数是均匀分布的，那么 60 大概会在区间 [50, 74] 中排名 40%）

计算区间频率以及最高排名

那么怎么计算每个区间的频率和最高排名呢？我们可以使用一个定时任务，通过轮询所有桶来更新每个区间的频率以及最高排名，我们叫这个为 global query，因为算法直观且简单，所以这里省略了计算的方法，有兴趣的读者可以从原文中了解。在实现中，我们使用了 Python NDB 客户端并且用 Memcache 当成 Datastore 的缓存。并把桶同时存储在 Datastore 和 Memcache 中，当计算排名的时候，先从 Memcache 中读取桶的数据（如果 Memcache 中没有则从 Datastore 中获取）。在这个算法中 FindRank和 SetScore的时间复杂度都为 O(1)，也就是和玩家数量无关，而 global query 的时间复杂度为 O(玩家数量) * 缓存更新频率，而且与桶的数量有关。

优点：

• 非常高效，即使返回的排名计算方式和 global query 的更新频率有关，但是一旦用户分数改变，那么排名也会马上会改变。
• 因为计算每个区间的最高排名是 global query 来定时实现的，所以用户的分数更新无需和桶的数据同步，所以我们能够支持玩家分数高并发更新。

缺点：

• global query 中计算所有用户的分数，计算全部排名以及更新桶的时间都需要考虑进去，在我们的测试中，在百万用户的数量级的时间是 8分34秒，这比用几个小时来计算每个玩家的排名要快得多。相反，之前的二叉平衡树算法能够快速地进行更新，虽然实现起来更加复杂以及对并发更新有限制。
• 在所有情况下，FindRank的速度同样依赖于从 Memcache 中获取数据的速度， 以及当缓存失效之后从 Datastore 中获取数据的速度。

准确率

这个算法的准确率取决于有多少个桶，玩家所在的排名，以及分数的分布。下图是使用不同桶情况的准确率，测试使用了 1万名玩家，以及 [0, 9999] 均匀分布的分数，下图可以看到，即使使用 5个 桶，错误率也在 1% 左右。

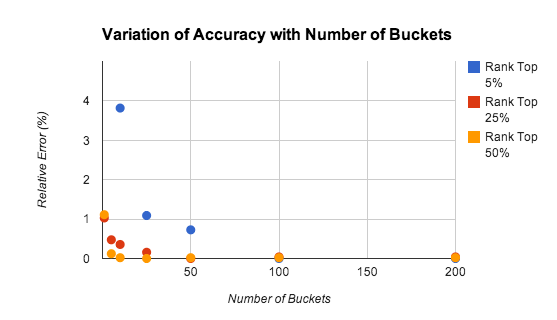
准确率在计算高排名玩家的时候会下降，大部分原因是因为大数定律不适用于仅仅关注高分数的时候。在很多时候，我们可以用一个更加准确的算法来维护这些玩家的排名（注释：例如高分数桶内进行插入排序）因为只有少部分的玩家需要这样计算排名，所以耗费的时间也很少。在上面的测试中，使用均匀分布的分数都能得到不错的效果，除此之外，对于任何密集的分数分布，使用此算法也能得到很好的结果，下图显示了在正态分布情况下预计和实际的排名差别：

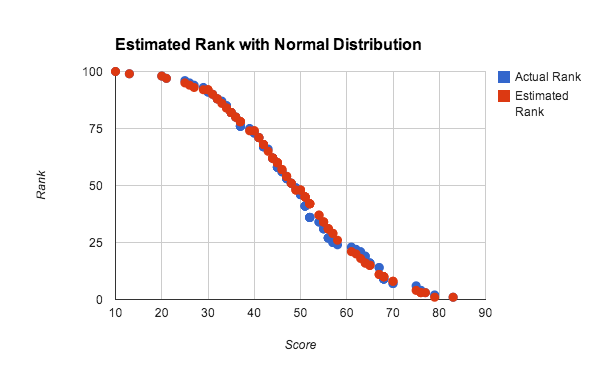
在这个实验中，我们使用了一个只有 100名 玩家的小数据集来测试准确率。每个分数是从 4 个 [0, 100] 的随机数的和的平均值组成，大致能生成一个正态分布的分数，上图使用的是 10个 桶来计算，我们可以看到算法在这个小数据集和非均匀分布的数据集下都能得到很好的结果。

结论： 这篇文章利用现实的例子从算法以及工程的角度分析解决方案，堪称系统设计的典范，其中提及的近似算法也能应用到其他类似的设计场景中，实在受益匪浅。